Alexander Rolle

I am a postdoctoral researcher in the Mathematics department at The Technical University of Munich, Germany, working with Ulrich Bauer.

Previously, I was a postdoc in the research group of Michael Kerber at TU Graz, Austria. Before that, I finished a PhD in Mathematics at The University of Western Ontario, Canada, supervised by Rick Jardine.

My research interests are in applied and computational topology, especially applications to statistics, data analysis, and machine learning.

For a complete list of publications, see my Google scholar page.

Selected research projects

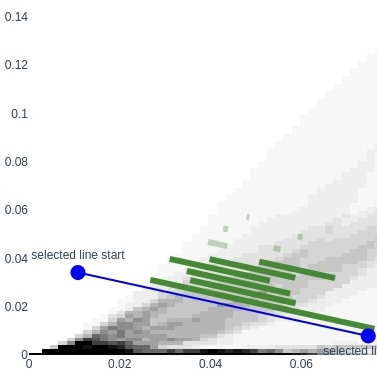
Persistable: persistent and stable clustering

Persistable is an open-source Python library that combines innovative hierarchical clustering algorithms with visualization tools from topological data analysis. With these tools, the user can tune parameters in an informed way, and get reliable clusterings that reflect stable features of the data. Persistable includes theoretically-justified approximation algorithms that provide massive reductions in memory usage compared to similar clustering methods.

Persistable is joint work with Luis Scoccola.

For an introduction to Persistable, see the documentation. The theory behind Persistable was developed in our paper Stable and consistent density-based clustering via multiparameter persistence, and the software is described in a paper in JOSS.

mpfree: fast minimal presentations

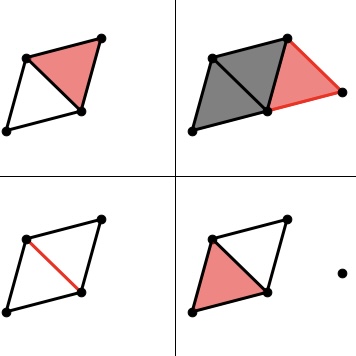
mpfree computes minimal presentations of two-parameter persistent homology. Multi-parameter persistent homology is a major topic of current research in topological data analysis: using multiple parameters makes it possible to analyze more complex scientific data, but also introduces challenges, especially for computation. A minimal presentation is a kind of compressed representation of a multi-parameter persistence module: this is desirable since input sizes in multi-parameter persistence tend to be huge.

mpfree is joint work with Michael Kerber. Our algorithm is an accelerated version of the method of Lesnick and Wright.

mpfree is available here. We published our work on mpfree at ALENEX 2021.

Topological analysis of 3D digital ovules

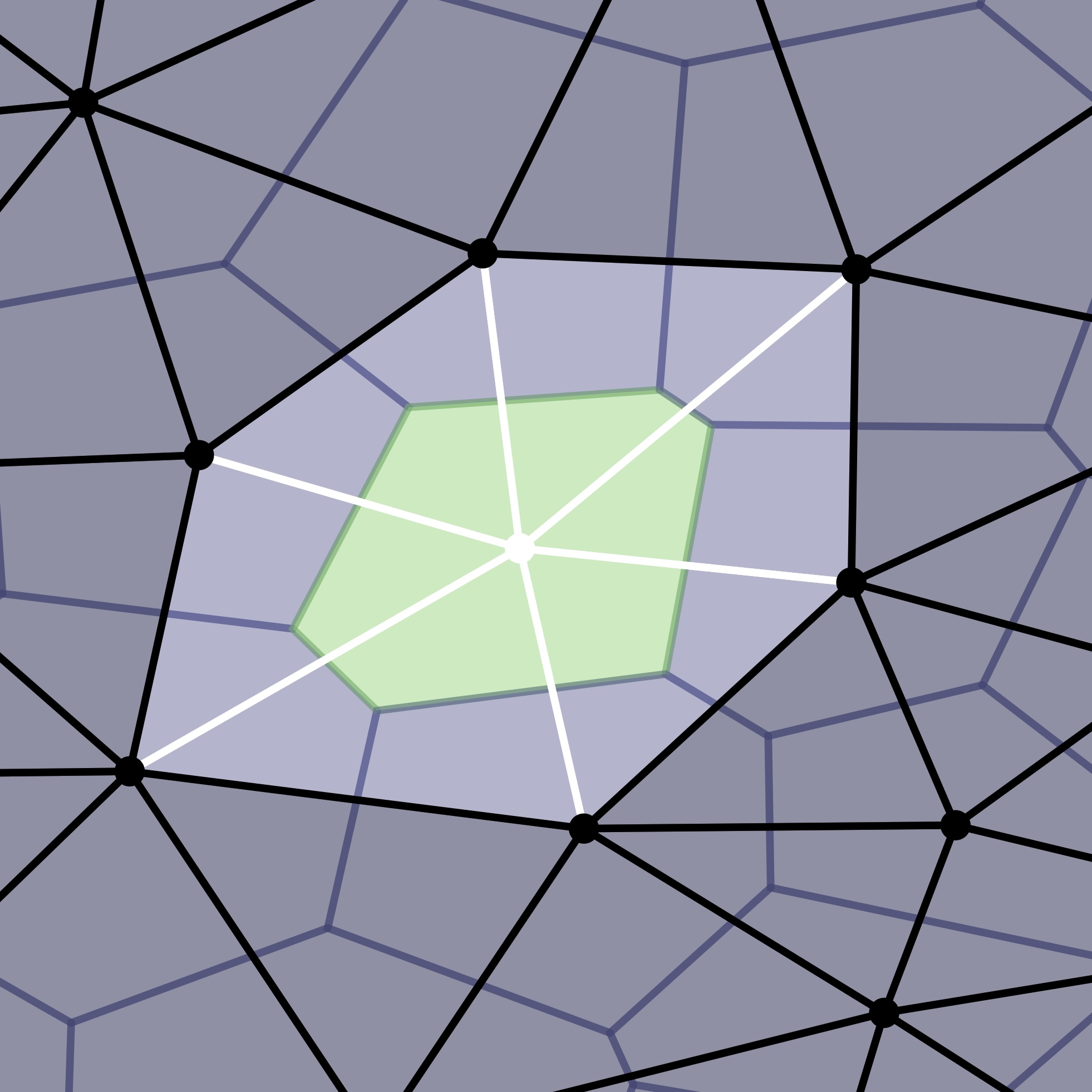
A basic problem in plant biology is tissue morphogenesis, in particular, the problem of how the 3D cellular architecture of a developing organ contributes to its final shape. We use the nerve construction from computational topology to detect differences in cellular architecture between homologous tissues of different species.

This is joint work with Nico Stucki, Fabian Roll, and Ulrich Bauer from the Applied and Computational Topology group at TUM, and Tejasvinee Atul Mody and Kay Schneitz from the Plant Developmental Biology group at TUM.

Our paper is available at Development.

Homology inference for degree-Rips

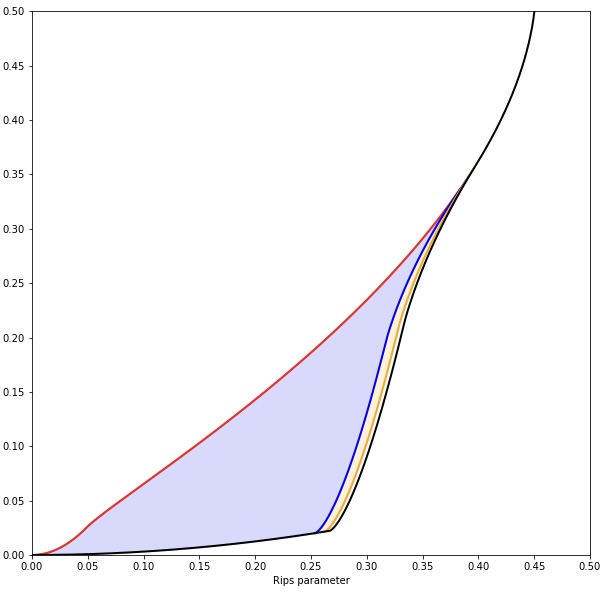
The degree-Rips bifiltration is a popular approach to density-sensitive multi-parameter persistent homology. Like the Vietoris-Rips filtration, this construction encodes the (geometric) shape of data, but in a way that is sensitive to density. Compared to Vietoris-Rips, the degree-Rips bifiltration is also more robust to noise and outliers in the input data. In order to make this precise, I computed the degree-Rips complexes of some probability spaces concentrated near an annulus. The figure shows the degree-Rips parameter space; the blue region is where we get the homotopy type of the circle, and the yellow region is where we get the homotopy type of the 3-sphere.

I published these computations at SoCG.